
Es gilt die sogenannten Knoten eines Graphen mit Farben zu versehen. Dabei muss man jedoch beachten, dass Knoten, die miteinander verbunden sind, nicht dieselbe Farbe haben dürfen.
Ziel ist es, eine Färbung mit möglichst wenigen Farben zu finden!
Graphen sind beliebte Objekte – nicht nur in der Mathematik sondern auch außerhalb der Mathematik. Wenn wir zum Beispiel ein Busliniennetz einer Stadt betrachten: da gibt es Haltestellen und Linienführungen zwischen diesen. Von manchen Haltestellen fahren mehrer Linien weg, von manchen weniger.
In so einem Graphen sehen wir sogenannte Knoten und Kanten (die die Knoten verbinden). Entsprechend der Vielzahl von Dingen und Situationen, die man mit Graphen darstellen kann, gibt es auch etliche Problemstellungen für Graphen, die man sich ausdenken kann bzw. die durch Anwendungen entstehen.
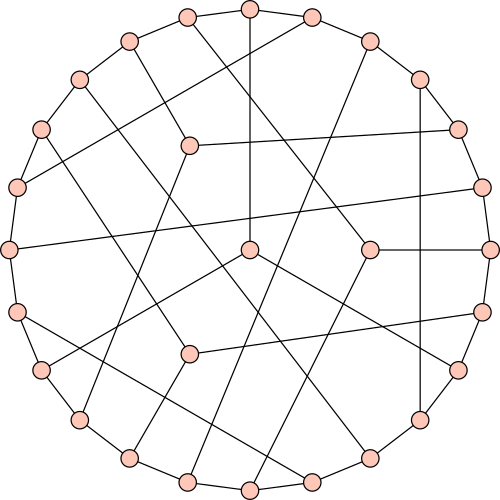
Eine beliebte Fragestellung ist die der Graphfärbung. Keine zwei Knoten, die durch eine Kante verbunden sind, dürfen die selbe Farbe haben. Ziel ist es, die minimale Anzahl von Farben zu finden, mit der so eine Färbung auf einem gegebenen Graphen realisiert werden kann. Diese Zahl nennt man die chromatische Zahl.
Allgemein gilt: das Finden der chromatische Zahl ist ein NP-vollständiges, also sehr schwieriges Problem.
Besondere Aufmerksamkeit wurde den sogannten planaren Graphen gewidmet. Dies sind Graphen, die man auf einem Blatt Papier zeichnen kann, ohne dass sich Kanten kreuzen. Für diese Grpahen gilt, dass 4 Farben jedenfalls ausreichen. Dieser berühmte Vierfarbensatz wurde in der Mitte des 19. Jahrhunderts als Vermutung aufgestellt, aber es dauerte mehr als 100 Jahre, bis der Satz tatsächlich bewiesen werden konnte.
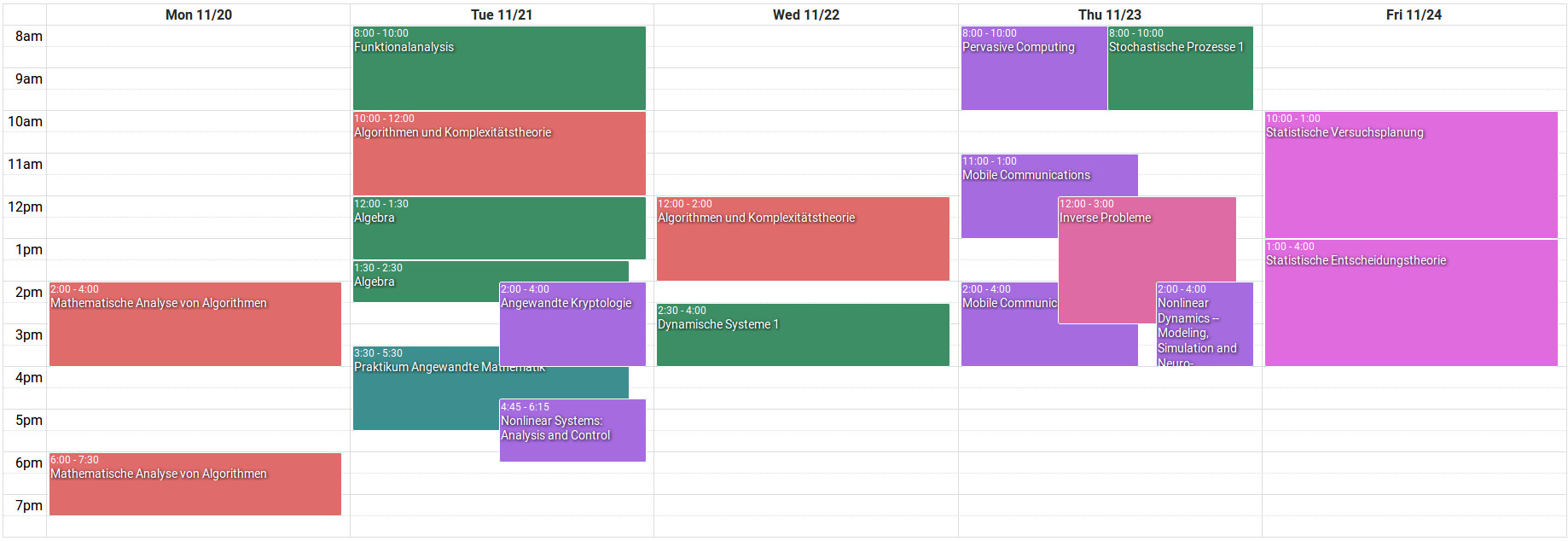
Das Erstellen von optimalen Stundenplänen ist eine der wichtigsten Anwendungen von Graphfärbung.
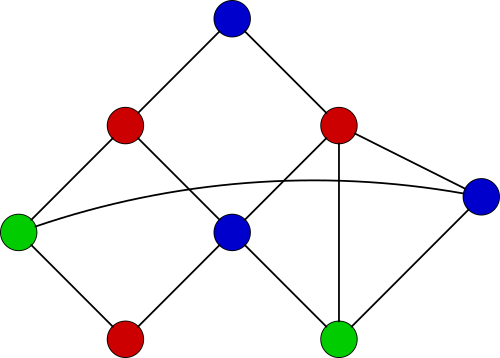
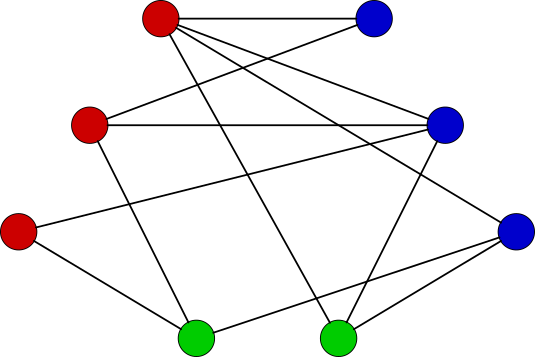
Mittels Graphfärbungen lassen sich allerhand mathematische Sätze beweisen, auch wenn man auf den ersten Blick meint, dass die Fragestellung nichts mit Graphfärbungen zu tun hat (z.B. das Museumswärterproblem).
Anwendungen finden sich aber natürlich auch außerhalb der Mathematik, zum Beispiel bei der Stundenplanerstellung. Jede Unterrichtsstunde entspricht einem Knoten im Graphen. Wenn gewisse Unterrichtsstunden nicht gleichzeitig stattfinden dürfen (weil der/die gleiche LehrerIn die Stunde hält), dann zeichnet man eine Kante zwischen diese Unterrichtsstunden-Knoten. Nach der Färbung des Graphen sieht man also, welche Unterrichtsstunden (nämlich gleichgefärbte) parallel abgehalten werden können.
Und auch der erwähnte Vierfarbensatz hat eine direkte Konsequenz für die Praxis: zeichnet man eine Landkarte und möchte jedes Land mit einer Farbe einfärben, sodass benachbarte Länder unterschiedlich gefärbt sind, so reichen 4 Farben dafür aus.